What's Recursion?

大家都學過高中數學，如果想用程式寫一個階層 5! = 5 x 4 x 3 x 2 x 1 = 120 怎麼做呢?

function recursion(a){
	return function(b = a - 1){
		return function(c =  b - 1){
			return function(d = c - 1){
				return function(e = d - 1){
						return a*b*c*d*e;
				}()
			}()
		}()
  }()
}
console.log(recursion(5)) // 120

恩，似乎是非常笨的方法，因為其實一直在重覆一樣的方法。那改成遞迴怎麼做呢 ?

function recursion (num){
	if(num == 1){
		return 1;
	}
	return num*recursion (num - 1);

}
console.log(recursion (5)); // 120

是不是簡潔多了！所以遞迴簡單來說就是

在函式之中呼叫函式自己本身

補充

之所以可以這樣寫，是因為函式堆疊（stack）在執行時是後進先出，當函式呼叫另一個函式時，需要等到裡面的函式執行完產生結果後，才會繼續回來執行自己的函式內容。

function first(){
	console.log('1')
	last();
	console.log('2')
}
function last(){
	console.log('3')
}
first() // 1 3 2

(推薦邦友寫的 Event Loop 機制)

若問題有同樣 pattern 在裡面，例如俄羅斯娃娃長得ㄧ模有樣只是尺寸會等比例變小、階層每一個數字都是前一個 - 1，就非常適合用遞迴解。遞迴好處就是程式碼簡潔好懂，但缺點就是效能通常會比較差。而且一定要設不再呼叫函式的條件防止無窮遞迴程式當掉

function recursion (){
	console.log('recursion ')
	recursion();
}
recursion(); // 哭哭 無窮遞迴

Big O (2^n) Fibonacci 費波那契

Fibonacci 是使用遞迴的著名例子，為了怕接下來文章太硬，就先來看個影片，證明演算法不只是紙上的數學而已。大自然隨處都可見 ! (講者講到臉上都在發光，我甚麼時候看演算法才能這樣)

看完之後應該對 Fibonacci 有個概念了，接下來就正式進到內文囉

Fibonacci 費波那契序列指的就是

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...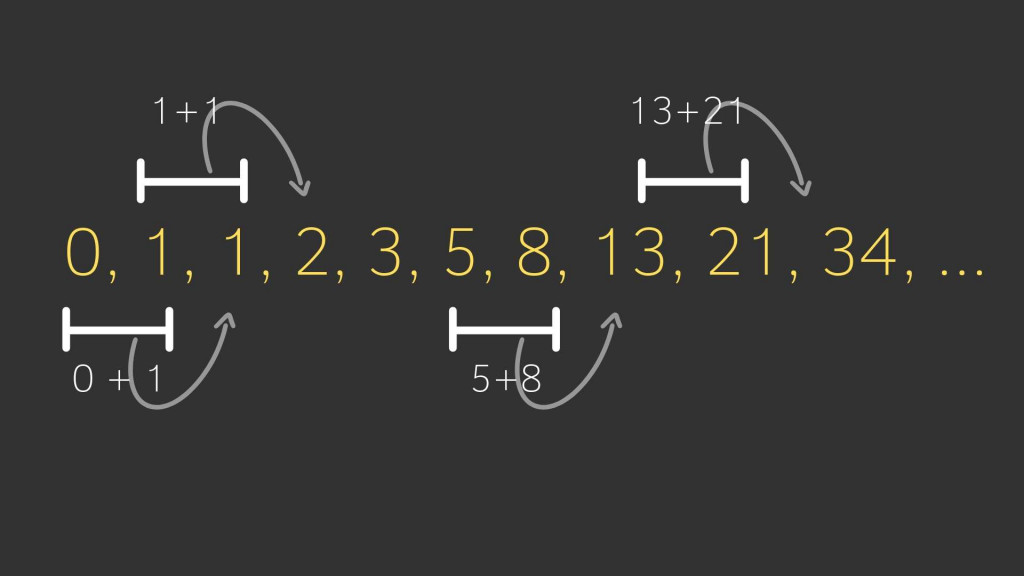

Fibonacci(0) : 0
Fibonacci(1) : 1
Fibonacci(2) : 1
Fibonacci(6) : 8

每個數字都是前兩個的總和, 0 + 1 = 1, 1+1 = 2, 2+1 = 3 以此類推

• 第 0 項 F(0) = 0
• 第 1 項 F(1) = 1
• 第 n 項 F(n ) = f( n-1 ) + f( n-2 ) // 第 n-1 項 + 第 n-2 項

觀察 Big O

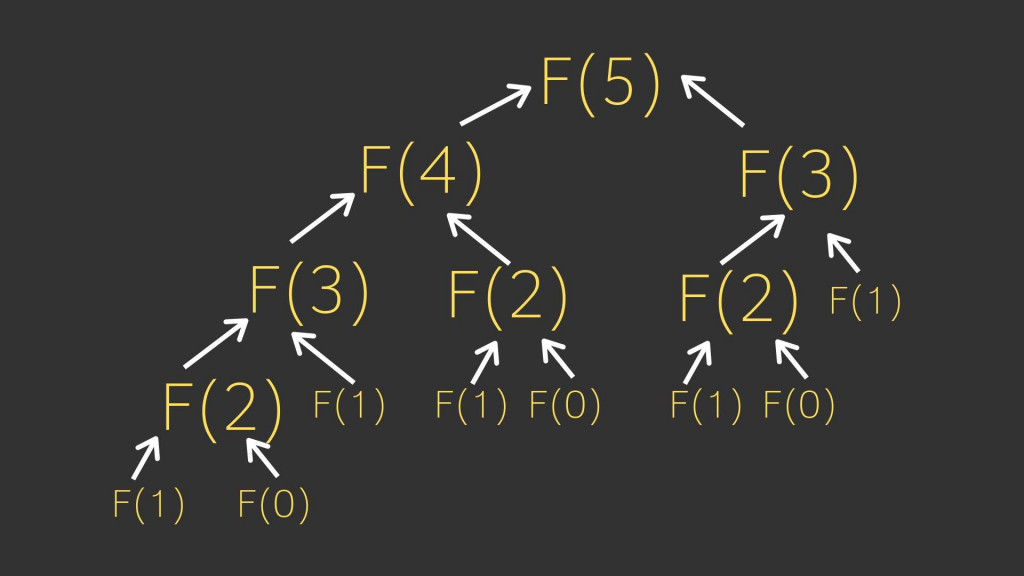
圖解 F(5) 如上圖

• 每次步驟變兩倍
• 總共有 n 層,
• 時間複雜度是 O(2^n)

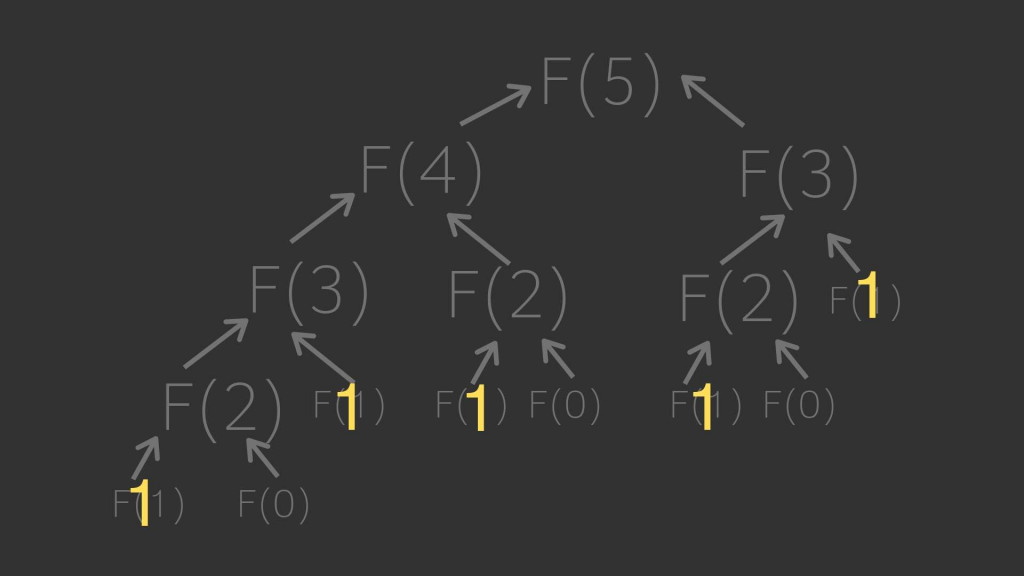
每一項都分成 f(n-1) + f(n-2) 一直拆到 f(1) = 1, f(0) =0 為止, 然後再把它全部加起來 (黃色數字) 就等於 5，而總共要執行 15 次這個函式

時間複雜度為 O(2^n) , 也就是 2 的 n 次方. 實際上來說這樣的執行速度非常慢, 例如 input 是 100 時，執行步驟會暴增到 30 位數．這樣的時間複雜度在設計演算法需要避免 (需要優化，例如存進 cache，明天篇章會提到 )

程式碼

function F(num){

	if(num == 0){
		return 0;
	}
    if(num == 1){
		return 1;
	}
	return F(num - 1) + F(num - 2)
}
F(5); // 5

如有錯誤或需要改進的地方，拜託跟我說。
我會以最快速度修改，感謝您

歡迎追蹤我的部落格，除了技術文也會分享一些在矽谷工作的甘苦。